Problema: Um terno elegante – Clubes de Matemática da OBMEP

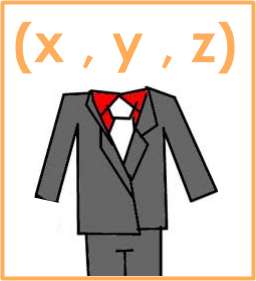
Problema Quando três números inteiros positivos x, y e z satisfazem a equação x^2+y^2=z^2, dizemos que (x, y, z) é um terno pitagórico. Prove que se (a, b, c\,) e (\,A, B, C) são ternos pitagóricos tais que aA-bB \gt 0 , então (aA-bB, aB + bA, cC) também é um terno pitagórico. Solução Temos

OBMEP 2019 - Nível 3 - Questão 1

Regulamento – O que é preciso para participar? – Clubes de Matemática da OBMEP

9o Ano Militar Apostila Matematica Vol 1 PDF, PDF, Números

Resolução de problemas

CONSEGUIR Matematica Lingua Portuguesa Professor-5ano 2017, PDF, Tetraedro

Inscrições – Clubes de Matemática da OBMEP

Estruturas Algebricas e Matemática, PDF, Conjunto (Matemática)

OBMEP 2022 - Nível 3 - Questão 11 - Alunos em Clubes

Portal Escola SESI

Prova obmep nivel 2 worksheet